Big O
We discussed Readability and Scalability are the two most important things to consider when writing code.
In this section, we will discuss Scalability in more detail.
Big O is the way to measure the scalability of an algorithm. At the same time, we are also able to know how efficient the algorithm is by Big O because the two key points to measure the efficiency of an algorithm are Time Complexity and Space Complexity.
- Readability
- Scalability
- Speed (Time Complexity)
- Memory (Space Complexity)
We can firstly focus on how to calculate the Big O of an algorithm. Then we will discuss how to improve the efficiency of an algorithm.
How to calculate Big O
Simply speaking, we can calculate the Big O of an algorithm by counting the number of operations the computer has to perform to run the algorithm.
A simple example:
// What is the Big O of the below function?
function anotherFunChallenge(input) {
let a = 5; // O(1)
let b = 10; // O(1)
let c = 50; // O(1)
for (let i = 0; i < input; i++) {
let x = i + 1; // O(n)
let y = i + 2; // O(n)
let z = i + 3; // O(n)
}
for (let j = 0; j < input; j++) {
let p = j * 2; // O(n)
let q = j * 2; // O(n)
}
let whoAmI = "I don't know"; // O(1)
}
// Answer:
// O(4 + 3n + 2n ) --> O(4 + 5n ) --> O(n)
So we know that the Big O of the above function is O(4 + 3n + 2n ). But we can simplify it to O(n) because we only care about the most significant term.
- What is the most significant term?
- Why do we only care about the most significant term?
Here is the place to introduce the Rule Book of calculating Big O.
Rule Book
There are only 4 rules in the Rule Book of calculating Big O.
Rule 1: Always worst Case
If we have a function that takes an array as input and returns the first element of the array, we can say that the Big O of this function is O(1) because it only takes one step to return the first element of the array.
BUT
If we have a function that takes an array as input, we assume the array has unlimited elements. so it will be O(n) when the function returns each element of the array.
Rule 2: Remove Constants
The obvious example of Remove Constants is the very first example we discussed.
O(4 + 3n + 2n ) --> O(4 + 5n ) --> O(n)
WHY
When we take Rule#1 into account meaning n gets to infinity, the constants will be negligible.
Rule 3: Different inputs should have different variables: O(a + b). A and B arrays nested would be: O(a * b)
- for steps in order
* for nested steps
Example
// What is the Big O of the below function?
function anotherFunChallenge(input1,input2) {
for (let i = 0; i < input1; i++) {
let x = i + 1; // O(a)
let y = i + 2; // O(a)
let z = i + 3; // O(a)
}
for (let j = 0; j < input2; j++) {
let p = j * 2; // O(b)
let q = j * 2; // O(b)
}
}
// Answer:
// O(a + b)
// What is the Big O of the below function?
function anotherFunChallenge(input1,input2) {
for (let i = 0; i < input1; i++) {
for (let j = 0; j < input2; j++) {
let p = j * 2; // O(b)
let q = j * 2; // O(b)
}
}
}
// Answer:
// O(a * b)
Rule 4: Drop Non-dominant terms (The same example as Rule#2)
Big O types
O(1) Constant - no loops
O(log N) Logarithmic - usually searching algorithms have log n if they are sorted (Binary Search)
O(n) Linear - for loops, while loops through n items
O(n log(n)) Log Linear - usually sorting operations
O(n^2) Quadratic - every element in a collection needs to be compared to ever other element. Two nested loops
O(2^n) Exponential - recursive algorithms that solves a problem of size N
O(n!) Factorial - you are adding a loop for every element
Iterating through half a collection is still O(n)
Two separate collections: O(a * b)
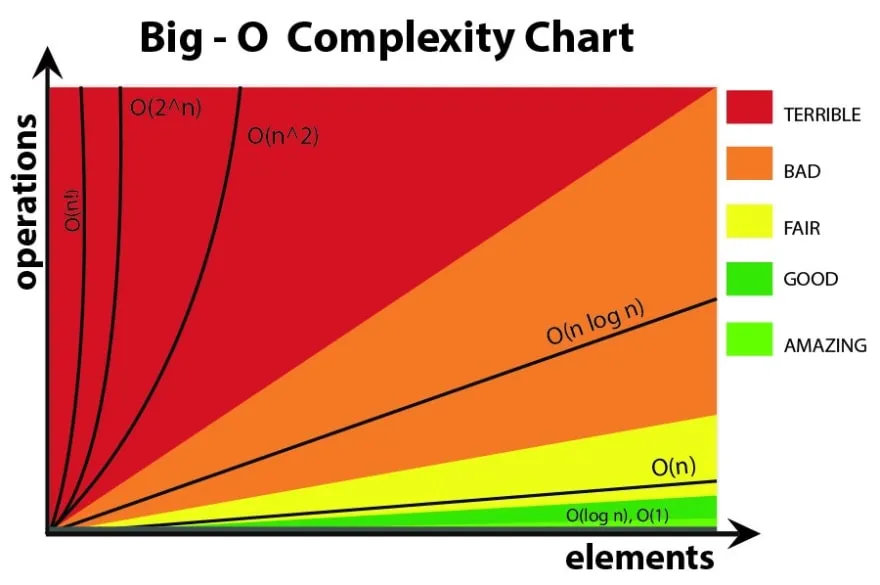
In this section, we only discuss the most common Big O types in our examples because the following types are mostly involved in certain algorithms.
- O(n log(n)) Log Linear - usually sorting operations
- O(2^n) Exponential - recursive algorithms that solves a problem of size N
- O(n!) Factorial - you are adding a loop for every element
Time Complexity
- Operations (
+,-, \*, /) - Comparisons (
<, >, ===) - Looping (
for, while) - Outside Function call (
function())
We can see the examples above.
Space Complexity
- Variables
- Data Structures
- Function Call
- Allocations
The rule to calculate the space complexity is similar as the time complexity.
function boooo(n) {
for (let i = 0; i < n; i++) {
console.log("booooo");
}
}
// #6 Space complexity O(n)
function arrayOfHiNTimes(n) {
var hiArray = [];
for (let i = 0; i < n; i++) {
hiArray[i] = "hi";
}
return hiArray;
}
arrayOfHiNTimes(6);